Est-ce que la résolution de certains problèmes complexes doit rester hors de portée de l’humanité ? Pour le bien de tous, parfois, on aurait préféré que oui :).
P = NP, ça n’a l’air de rien, mais c’est le problème fondamental des mathématiques et de l’informatique théorique depuis plus de 50 ans.Dans cet article, vous comprendrez facilement « P = NP », pourquoi ce problème est important et les implications de sa résolution ou de son impossibilité.
Comprendre P = NP : la petite histoire
Imaginez que vous devez assembler seul un puzzle d’un million de pièces. Il s’agit d’un problème extrêmement difficile, dans la mesure, où trouver la bonne combinaison entre chaque pièce peut prendre une éternité. On estime qu’un tel puzzle « pourrait » être résolu en équipe après plusieurs années en travaillant huit heures par jour.
Il en va de même pour un ordinateur résolvant des problèmes complexes. Certaines énigmes demandent une capacité de calcul si élevée que le problème est soit insoluble ou soluble après une très longue période de temps.
Et pourtant, il y a un paradoxe. Bien qu’assembler un puzzle d’un million de pièces soit un problème extrêmement difficile, sa résolution est très rapide. En effet, il suffit simplement de voir ce puzzle terminé pour valider ou non la solution.
La question se pose alors : est-ce qu’un problème facile à trouver (P) est égale à un problème facile à vérifier (NP) ? Si c’est le cas, nous mettrions autant de temps à assembler un puzzle d’un million de pièces que pour le vérifier. La résolution de ce problème permettrait une amélioration considérable de nos possibilités en calcul informatique.
Qu’est-ce que P ?
P signifie « facile à trouver« . Il représente l’ensemble des problèmes pouvant être résolu très rapidement. Si on reprend la métaphore du puzzle, P serait un puzzle extrêmement facile à assembler (comme un puzzle composé d’une pièce).
P en termes techniques
Tous les problèmes qui appartiennent à P, sont les problèmes pour lesquels il existe un algorithme polynomial. C’est-à-dire, au plus et dans le pire des cas, le nombre d’étapes de communication est inférieur ou égal à un polynôme (≤ O(n log n)), une puissance constante de n à la taille d’entrée au problème.
Ce qui veut dire, en termes simples, que le temps de résolution d’un problème est proportionnel à la taille du problème (le nombre de pièces du puzzle ou la taille du polynôme en terme scientifique). Plus le nombre de pièces dans un puzzle est élevé et plus la durée de résolution de ce puzzle sera considérable.
Qu’est-ce que NP ?
NP signifie « facile à vérifier« . Il représente l’ensemble des problèmes pouvant être vérifié rapidement. Si on reprend la métaphore du puzzle, NP serait n’importe quel puzzle, car il est aisé de trouver les incohérences dans l’assemblage de celui-ci. Bien que leurs résolutions soient simplement vérifiables, ils peuvent être difficiles à résoudre. Cela dépendra de la taille du problème (N = le nombre de pièces du puzzle).
NP en termes techniques
Un problème appartenant à la classe NP, a au moins un algorithme qui le résout (lentement) de façon exponentielle (e^x), mais sa vérification peut se faire de façon polynomiale (donc rapidement).
Expliqués simplement, les problèmes NP (comme le puzzle) ont un temps d’exécution exponentiel (chaque pièce ajoutée au puzzle élargit sa durée de résolution de manière exponentielle). Néanmoins, ils ont un temps de vérification polynomial, par conséquent, le temps requis pour vérifier la solution n’augmente pas aussi vite que le temps requis pour résoudre le problème.
Les NP complets
Reprenons notre histoire de puzzles, les NP complets sont des puzzles effroyablement difficiles à résoudre. En revanche, si l’on arrive à résoudre l’un d’entre eux, on peut résoudre tous les autres. L’enjeu est donc de trouver la formule capable de résoudre tous les problèmes NP en un temps record. C’est pour cela que les mathématiciens se penchent sur la résolution d’un NP complet. Résoudre un NP complet permettrait la résolution de tous les problèmes NP.
Pourquoi ce problème vaut 1 million de dollars ?
Résoudre P = NP nous permettra de créer un algorithme capable de résoudre des problèmes ayant un temps d’exécution exponentiel à la vitesse d’une exécution polynomiale. Si cela est possible, ce serait une grande révolution informatique et en mathématiques, nous pourrions ainsi décupler la capacité de calcul de nos machines avec beaucoup moins de ressources. Mais, également résoudre des problématiques que nous pensions insolubles.
Qu’est-ce qui changerait si P était égal à NP, ou si P était différent de NP ?
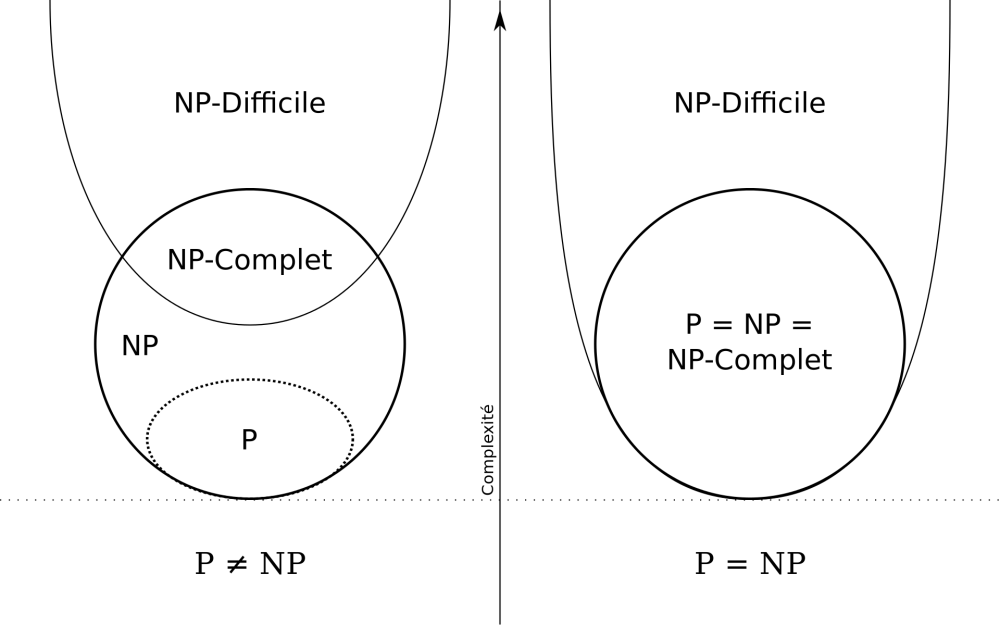
Si P = NP
En informatique
Une immense économie de ressource. En effet, s’il est possible de réduire radicalement la durée de résolution de problèmes complexes, mais simples à vérifier. Nous pourrions produire une quantité phénoménale de produits digitaux à moindre coût.
Dans la cybersécurité
Si P = NP, les systèmes cryptographiques actuels (hash, cryptage symétrique, asymétrique…) deviendraient obsolètes, ce qui entraînerait une refonte totale de la cybersécurité. En effet, le principe des algorithmes de cryptage est fondé sur le fait que l’on puisse rapidement les calculer (par exemple déchiffrer avec une clé), mais la résolution du problème sans la clé est très longue.
En intelligence artificielle
Les algorithmes d’apprentissage seront plus puissants et nécessiteront moins de ressources. De nombreux problèmes d’optimisation sont « NP-hard« . Si P = NP, la vitesse d’apprentissage et de raisonnement des algorithmes sera considérablement réduit.
En bioinformatique
P = NP permettra des progrès significatifs dans le domaine du séquençage de l’ADN, la génétique, la phylogénétique ou encore la création de médicaments. Là encore, cette équation pourrait permettre la création d’une grande quantité d’innovations.
Impact sur l’économie
Les entreprises du monde entier optimiseraient parfaitement leurs processus, ce qui se traduirait par d’immenses gains en productivité. De nombreux problèmes de théorie des jeux sont « NP-hard« . Si P=NP, nous pourrions facilement trouver les équilibres de Nash pour comprendre les interactions stratégiques en économie, en sciences politiques et dans d’autres sciences sociales.
Si P ≠ NP
Il serait donc impossible de résoudre des problèmes à temps d’exécution exponentiel de manière polynomiale. Il serait alors fondamentalement plus difficile de résoudre un problème que de vérifier sa solution (ce qui est le cas intuitivement). Même si nous perdons en productivité, cette conclusion garantit nos systèmes de sécurité informatique. La validité des systèmes comme la cryptographie à clé publique ou la sécurité bancaire seraient assurés.
